
Bahtsız kral Sisifos’u bilir misiniz? Antik Yunan mitleriyle ilgilenenler için bu isim çok yabancı olmasa gerek. Tanrıları çeşitli sebeplerden kızdırması üzerine Hades’in toprağında sonsuz bir cezaya mahkum edilir Sisifos. Mahkum kralın cezası çetindir. Özgürlüğü, zorlukla yerinden kımıldatılabilen dev bir kayayı dik bir tepenin doruğuna çıkarmasına bağlıdır.Sisifos sadece kaya doruğa erişebilirse azat edilecektir.
Lakin mahkum ruha tanrıların duyduğu nefret öyle hafif bir nefret değildir, kısıtlı fani ömründe ortalığı az karıştırmamıştır Sisifos. Bu sebeple cezaya ilahi bir “bug” eklenir: Sisifos kayayı ne zaman doruğa ulaştırsa, son anda kaya elinden kayacak ve tüm yokuş boyu yuvarlanıp başladığı noktaya dönecektir. Sisifos’un bu durumun bilincinde iken neden inatla kayayı tepeye doğru itelemekle uğraştığını kimse bilmez. Muhtemelen siz bu yazıyı okurken o hala görevini icra etmekle meşgul. Bugün İngilizce’de “a sisyphean task”; anlamsız ve sonu gelmeyen, aşırı yorucu işleri tanımlamak için kullanılır (Mesela 2014’te hala inatla WoW oynamak).
Geçen hafta oyun finallerinden bahsettik ama “finalsiz oyunlar” üzerine hiç konuşmadık. Şahsi fikrim, bir video oyunu manalı kılan, bir noktadan sonra bitebilmesidir. Eğer oyun bitmemeyi esas almış, finali oyuncunun bir noktadan pes etmesine dayalı bir yapıya bürünmüşse tehlikeli sularda yüzüyoruz demektir. Bu sebeple Minecraft ve klonlarından ürkmüyorum desem yalan olur.
Şimdi “oyunlar ve sonsuzluk” deyince 2014’te akla ilk Minecraft (ve belki de son aylardaki çılgınlıktan ötürü Flappy Bird) geliyor. Ne var ki oyunseverler bu soruyu 1990’ların başında bile soruyorlardı, hem de çok tanıdık başka bir bağımlılık yüzünden: Tetris. 1984 yılından beri her konsolda kendine yer edinen Tetris’i bilmeyenimiz yok. Ancak geçen otuz yılda “Tetris’in sonu var mı?” sorusu halen tam anlamıyla cevabını bulmuş değil. Evet, kaçınız bu meseleye kafa patlattı?
Tetris’i diğer skor tabanlı oyunlardan ayıran birkaç özellik bulunmakta. En önemlisi oyunun temelde bir puzzle/bulmaca olması. Bir bulmaca, doğası gereği çözülebilir olma hissi uyandırır. Bulmacalarda hatalı hareketler sizi çözümsüz noktalara da çekebilir, ancak tetris oyuncuya hatalarını düzeltme şansı veren, bir nevi hata payı bırakan bir oyun. Bu sebeple meraklısı için oyunun üzerinde her koşulda sonuç veren bir algoritma bulmak cazibeli bir uğraş. Oyunun ikinci büyük özelliği ise eskiden beri süregelen popülaritesi. 90’larda Nintendo Gameboy’una duyduğumuz açlıktan ötürü anne babalarımız tarafından alınan sayısız korsan Tetris konsol(umsu)larını hatırlayın. Ve bu konsollar olayın sadece Türkiye ayağıydı, kim bilir dünyada nasıl bir çılgınlık dönüyordu.
Şimdi konu hakkında yazılıp çizilmiş olaylara bir göz gezdirelim. Tetris algoritmalarına kafa yormuş bir miktar matematikçi bulunmakta ve ilk çalışma 1992 yılına uzanıyor. Waterloo Universitesi’nde John Brzustowski’in hazırladığı yüksek lisans tezi (Can You Win At Tetris?, 1992), sabit hızda devam eden (yani skor büyüdükçe hızlanmayan) bir tetris oyununun sonsuza kadar sürdürülebilir olup olmadığını sorguluyor (Teorik değil de uygulamalı matematik alanında bir tez olmasından ötürü Brzustowski’nin işi biraz emek harcanıldığında matematikçi olmayanlar tarafından da anlaşılır nitelikte, vakit bulursanız okuyun).
Brzustowski, tezinde basitten yola çıkarak yedi tetronimonun (tetris şekilleri) bir arada olduğu oyunları değil de, bu yedinin ikili permütasyonlarını alıp oyunu kuruyor; yani sadece çubuk ve karelerden oluşan bir oyun ya da sadece S ve Z şeklindeki tetronimolardan bir oyun vb… Bu oyunlarda gelinen sonuca göre eğer A.I. oyuncuyu “yenmek” isterse, yapması gereken tek şey çok yüksek miktarda S ve Z tetronimosu göndermek.
Bir başka matematikçi Heidi Burgiel, Brzustowski’nin (bu adı bir kez daha yazarsam çıldıracağım!) tezine destek niteliğinde olan “How to Lose Tetris?” adlı makalesinde teorik olarak bir oyunu yenilgiye mahkum bırakmak için kaç adet S ve Z gerektiğini hesaplıyor (Burgiel, Mathematical Gazette, 1997, vol 81, 194-200). Burgiel’in hesaplarına göre sadece S ve Z’lerden oluşan bir oyunda mutlak yenilgi için 69.600 tetronimo gerekmekte. Normal herhangi bir tetris oyununu bitiren hamle ise 127.200 adet S ve Z’nin ardarda gelmesi! Burgiel’in hesaplamasının sonunda dediği gibi “Tetris’te kaybetmek aslında kolay, sadece çok uzun zaman gerekiyor.”
Tabii gerçek hayatta bu kadar yüksek sayılarla işimiz yok. Sadece S ve Z üzerine kurulu bir oyunda iyi tetris oyuncularının yenilmeden dayanma süreleri 150 tetronimo. Ancak 150 S/Z tetronimosunun bile ard arda gelme ihtimali (2/7) üzeri 150!
Gene de bizim aradığımız çok küçük de olsa bir ihtimal olup olmadığı idi ve bu ihtimale ulaştık. Peki bu durum tetrisi bir sispyhean task olmaktan çıkarıyor mu? Tam değil. Normal tetris oyunları bu çok düşük olasılığın vuku bulmaması için tetronimoları sıraya dizen “random generator”lar kullanıyorlar. Bu random generatorlar çeşit çeşit, ancak büyük çoğunluğunun ortak özelliği, içinde her bir tetronimo tipinden bir adet bulunan setler düzenleyip onları öyle oyuna sürmeleri. Mesela random generator “S-T-Z-L-O-I-J” şeklinde bir set yapıyor ve tetronimolar bu sıra ile tepeden düşmeye başlıyorlar. Yani üstüste ikiden fazla S ya da Z görmemize imkan yok (Bir setin sonu ile sonraki setin başı şans eseri aynı olabilir ). Random generatorlar tüm taşları farklı sıralarla oyuna sürerken ne kadar mı değişik yol izleyebilir? Basit bir hesapla 7! yani 5040 adet.
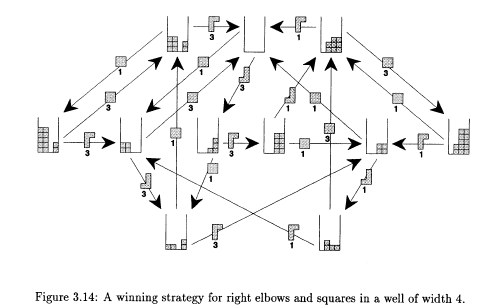
An itibariyle mevcut Tetris oyunlarını sonsuza kadar oynamak için geliştirilmiş tek bir teknik bulunmakta. Dileyenler şu linkten tekniğe ulaşabilirler. Ne var ki bahsedilen strateji sadece 2001’den sonra çıkan ve kısmen modifiye edilmiş tetris oyunları için geçerli. Bu oyunlarda “Hold” seçeneği ile beğenmediğimiz bir tetronimoyu kullanmama hakkına sahibiz. Bu avantajla bile tetrisi sonsuz döngüye bağlamak için her seferinde 140 tetronimodan oluşan bir stratejiyi uygulamalıyız. Tetris hayranları bu sayıyı azaltacak ve “Hold” özelliğine ihtiyaç duymayacak yeni teknikler peşindeler.
Özetle durum böyle sevgili geekyaparlar. Sisifos hala dev kayasını itmekle meşgul. Belki de şu an kayanın peşinden yokuş aşağı koşturuyordur, kim bilir? Görülen o ki, tetrisseverler ne kadar ustalaşırlarsa ustalaşsınlar hala lanetli kralın yolundan gitmiyorlar. Teorik olarak minnacık, pratikte ise kocaman bir “game over” Tetris’te hala suratımıza çarpıyor. Belki bir gün bitmeyen Tetris formülüne ulaşacağız, Youtube’u haftalar süren oynanış videolarıyla dolduracağız. Ama o güne bell ki daha çok var. Seviyorum seni Tetris, şirin tetronimoların ve otuz sene boyunca insanlara yaşattığın heyecan için. Ama en çok “bitmesini bilen” bir oyun olduğun için…



